Set (game)

Set! redirects here. Set! is also a special form in the Scheme programming language.

Set is a real-time card game designed by Marsha Falco in 1974 and published by Set Enterprises in 1991. The deck consists of 81 cards varying in four features: number (one, two, or three); symbol (diamond, squiggle, oval); shading (solid, striped, or open); and color (red, green, or purple).^[1] Each possible combination of features (e.g., a card with three striped green diamonds) appears precisely once in the deck.

1 History
2 Games
3 Basic Combinatorics of Set
4 References
5 External links

History

The game evolved out of a coding system that the designer used in her job as a geneticist.^[2] Set won American Mensa's Mensa Select award in 1991 and placed 9th in the 1995 Deutscher Spiele Preis.

Games

Several games can be played with these cards, all involving the concept of a set. A set consists of three cards which satisfy all of these conditions:

They all have the same number, or they have three different numbers.
They all have the same symbol, or they have three different symbols.
They all have the same shading, or they have three different shadings.
They all have the same color, or they have three different colors.

The rules of Set are summarized by: If you can sort a group of three cards into "Two of ____ and one of _____," then it is not a set.

Given any two cards from the deck, there will be one and only one other card that forms a set with them. One example of a set would be these three cards:

One red striped diamond
Two red solid diamonds
Three red open diamonds

In the standard Set game, the dealer lays out cards on the table until either twelve are laid down or someone sees a set and calls "Set!" The most cards you can lay out are 15. The player who called "Set" takes the cards in the set and the dealer continues to deal out cards until twelve are on the table. If a player sees a set among the twelve cards, they call "Set" and take the three cards, and the dealer lays three more cards on the table. It is possible that there is no set among the twelve cards; in this case, the dealer deals out three more cards to make fifteen dealt cards, or eighteen or more, as necessary. This process of dealing by threes and finding sets continues until the deck is exhausted and there are no more sets on the table. At this point, whoever has collected the most sets wins.

Basic Combinatorics of Set

Given any two cards, there exists one and only one card which forms a set with those two cards. Therefore the probability of producing a Set from 3 randomly drawn cards from a complete deck is 1/79.
The largest group of cards you can put together without creating a set is 20.^[3]
There are 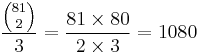$\frac{{81 \choose 2}}{3} = \frac{81 \times 80}{2 \times 3} = 1080$ unique sets.
If 26 Sets are drawn from a collection of 81 cards, the remaining 3 cards form a Set too.
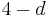The probability a set will have $d$ features different and $4-d$ features the same is 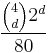$\frac{{4 \choose d}2^d}{80}$ (Note: d=0 all four features the same is impossible as no two cards are identical). Thus, 10% of possible sets differ in one feature, 30% in two features, 40% in three features, and 20% in all four features.
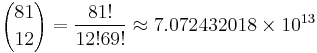
The number of different 12-card deals is ${81 \choose 12} = \frac{81!}{12! 69!} \approx 7.072432018 \times 10^{13}$
The odds against there being no Set in 12 cards when playing a game of Set start off at 30:1 for the first round. Then they quickly fall, and after about the 4:th round they are 14:1 and for the next 20 rounds they slowly fall towards 13:1. So for most of the rounds played, the odds are between 14:1 and 13:1.^[4]
The odds against there being no Set in 15 cards when playing a game are 88:1.^[4]
Around 30% of all games always have a Set among the 12 cards, and thus never need to go to 15 cards.^[4]
The average number of available Sets among 12 cards is 2.4 and among 15 cards 3.3.^[4]

References

^ "How to Play Set". http://www.setgame.com/set/rules_set.htm.
^ http://www.setgame.com/set/history.htm
^ Benjamin Lent Davis and Diane MacLagan. "The Card Game Set". http://www.math.rutgers.edu/~maclagan/papers/set.pdf.
^ ^a ^b ^c ^d "SET Probabilities Revisited". http://henrikwarne.com/2011/09/30/set-probabilities-revisited/.

External links

Set Enterprises website
A Mathematic exploration of the game Set . Including 'How many cards may be laid without creating a set', as well as investigations of different types of set games (some in the Fano plane).
MultiplayerSet – realtime javascript-powered browser version
Set! ME – Java enabled mobile phone version
Set at BoardGameGeek
3qual A single-player set play-alike web page and Android app.
Set at Smart-Games Single and multiplayer